什么叫做有限小数和无限循环小数

*** 次数：1999998 已用完，请联系开发者***

∪０∪ 一米长物体能否完美三等分?揭秘1/3的无限奥妙!最简单的解释是:不要总是纠结于0.3333.(无限循环),你直接接受1/3不就行了吗?1/3乘以3不就刚好等于1吗?为何非要把所有数写成小数形式才甘心呢? 但总有人就是不甘心,非要用小数表达才罢休。于是问题的关键就在于:0.9999.是否等于1? 0.9999.等于1,0.9999.等于1,0.9999.等于1。重...

(ˉ▽ˉ；)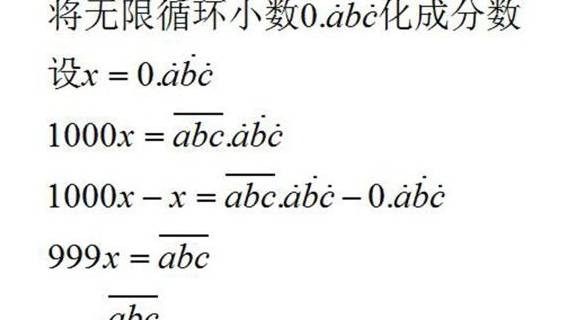

圆周率π能否完全算出?如果可以会发生什么惊人变化?圆周率π是一个众所周知的无理数,这意味着它是一个无限不循环的小数。由于其无限不循环的特性,π无法被完全精确地用小数表示出来。 实... 尽管π不能用有限的小数完全表示,但这并不意味着它是一个不确定的数字。相反,π是一个固定不变的值,正如“1就是1”那样明确无误。 如果...

圆周率π的终极谜题:能否被完全算出?若真算尽,后果将如何?圆周率π,众所周知是一个无理数。所谓无理数,指的是一个无限不循环的小数。由于它是无限且不重复的,因此无法用有限的小数形式完全准确地表示出来。 实际上,“被完全算出”这一说法本身就不够严谨,带有较强的主观色彩。所谓的“完全算出”并不意味着必须用小数点后的每一位...

╯０╰

回顾:圆周率隐藏什么秘密?已算至62.8万亿位,若被算尽会发生什么?如果圆周率被算尽,世界将会发生什么不可预知的事情?是如同像打开潘多拉魔盒一样?还是物理定律被打破,数学公式被推翻?对于圆周率的概念,大家的第一反应都会想到π,因为在数学上,圆周率属于一个无理数,也就是属于无限不循环小数,它是用来定义圆形之周长与直径之比值,从古至今...

圆周率之谜:普朗克长度揭示的无限分割悖论永不重复的小数,它与进制无关。 在数学领域中,我们把π称为无理数,意指它不能表示为两个整数的比例。除了π,√2、√3、√5等也是无理数,它们的小数部分无限延伸。圆的魅力引领我们发现了π,它代表圆周长与其直径的比率,这个比率恰恰是一个无限循环的常数。 为了逼近π的精确...

圆周率的尽头在哪里?普朗克长度揭示的极限与无限分割之谜永不重复的小数,它与进制无关。 在数学领域,我们把π称为无理数,这意味着它不能表示为两个整数的比例。除了π,√2、√3、√5等也是无理数,它们的小数部分无限延伸。圆的魅力引领我们发现了π,它代表圆周长与其直径的比率,这个比率恰恰是一个无限循环的常数。 为了逼近π的精...

∩ω∩

˙＾˙ 探索宇宙奥秘:圆周率的无尽之谜与普朗克长度下的极限挑战这个问题相当有趣,让我们先来回答第一个问题:圆周率π是一个无限不循环的小数,它与进制无关。 在数学领域,我们称π为无理数,这意味着它... 特别是对于那些被称为超越数的数来说,它们不能用有限的公式表达出来。例如,尽管刘徽的方法试图通过不断增加多边形的边数来逼近真实的...

?△?

?＾? 新纪录诞生:圆周率精确到小数点后105万亿位众所周知,圆周率π是一个无限不循环小数。 一般来说,我们会选择3.14来使用,而用十位小数3.141592653便足以应付一般计算,即使是工程师或物理学家要进行较精密的计算,充其量也只需取值至小数点后几百个位,不过近日,有人将它的小数点后105万亿位给算出来了。 据美国趣味科学网...

圆周率的尽头在哪里?普朗克长度揭示的极限,是科学的终点还是起点?永不重复的小数,它与进制无关。 在数学领域中,我们把π称为无理数,意指它不能表示为两个整数的比例。除了π,√2、√3、√5等也是无理数,它们的小数部分无限延伸。圆的魅力引领我们发现了π,它代表圆周长与其直径的比率,这个比率恰恰是一个无限循环的常数。 为了逼近π的精确...

?﹏?

圆周率π能被完全算出来吗?如果算尽了会怎么样?圆周率π,我们都知道它是一个无理数。何为无理数?就是无限不循环小数,既然是无限不循环,当然是不可能被完全算出来的,不可能用小数准确... 这说明什么?说明了一个无限的概念,圆的周长永远会无限地逼近一个值,但是永远到不了这个值,也就是说不存在真正意义上的圆。 人类历史上...